
Cartesian
2D Wave Equation

Cartesian Coordinates
This section will discuss vibrations in two dimensions. If you haven't already, take a look at the 1D wave equation. Modeling vibrations in two dimensions follows a very similar process but instead models the vibrations across a surface, such as a membrane.

The Equation:


This is the acceleration of the wave
The change in the slope of the membrane
This is the tension of the membrane divided by the density of the membrane. You use tension because it is the only force acting upon the membrane and density since it is mass per unit volume. *Think Newton's first law!*
What Does This Mean?
From the derivation we know that the wave equation is really just Newton's first law:
This can be rewritten as:
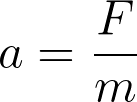
And with a little substitution we get the relationship between the acceleration of the membrane, the mass, tension, and the slope of the membrane:

Which really just means
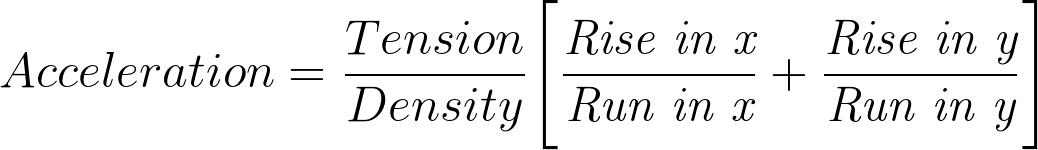
where

Thus you have:

Initial Conditions
The initial conditions are what the displacement of the membrane looks like at time = 0
Low Point
.png)
High Point
This means that the surface has an initial displacement - showing which parts are high and low
Boundary Conditions
The x and y in the boundary condition will give where the boundary is enacted. For an example, if we have an 1 by 1 membrane and the boundary condition has x=1 then the condition is true for the rightmost side of the membrane.


When the function is a constant this means that it is being held at a constant displacement. When the function is positive it means that the plate is being stretched at that location and when the function is negative it means that the plate is being depressed at this location.
When the function is any combination of positive and negative values (often sine or cosine) the plate is being stretched or depre the value of the function along that line.

Chladni Patterns (also called "Chladni Figures") are a popular demonstration tool for the visualization of mechanical vibration, and refer to the designs that form on a membrane when an external driving force is used force the system into resonance vibration, causing a series of standing waves to form within the plate. Below is a Mathematica script where you can explore an interesting 2D Wave Equation problem