
1D Wave Equation

Is 1D even relevant?
Absolutely; the 1D wave equation can be used as an abstraction to describe the behavior of a wire when plucked. The wave equation as visualized here has fixed boundary conditions and in initial horizontal velocity component.
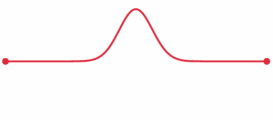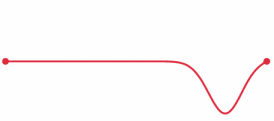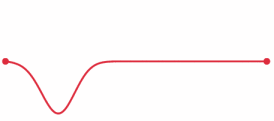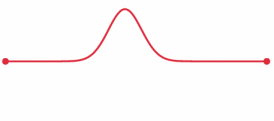
Source: Wikipedia Commons
The Equation:
This is the acceleration of the wave.
This is the change in slope of the wave.
The squared velocity that the wave can move along the wire.

Ok so what makes it do that?
This example of the wave equation does not have any damping terms and assumes no mass of the wire and and that everything obeys Hooke's law.
The PDE also takes initial and boundary conditions which will be described in the next section.
Initial Conditions
The initial conditions are the wire will look like at t = 0
This will mean that the line will initially have the shape of some function (in this case, a simple impulse given by the first derivative of the error function shown below.)

A.
B.
This will mean that the line initially has Initial velocity described by some function. In the case of the gif, the initial velocity is horizontal and is simply given by the derivative of the initial shape. This results in translation to the left. There is a more realistic example of a 'plucked' string in the linked interactive notebook below.
.png)
A. Negative velocity means points here move down with time
B. Positive velocity means points here move up with time
Boundary Conditions
This means that the function must go to zero at points 0 and 1 on the line for all times. Physically you could imagine a string of length 1 fixed at both ends. Different boundary conditions can be used to model different things. For example, where the derivatives of u are zero, this could be used to model waves in a trough of water.